Introductory work on Spectral Theory

The original motivation of spectral theory is to classify (linear) operators. Then, as a property of operators, spectrum could be applied to describe the operators. For complicated PDE systems, it is very efficient to look at its spectrum to understand it, without dirty computation for a numerical solution. With Prof. Alexander Strohmaier, I considered the impact of boundary on operators, the insights from eigenvalue and eigenfunctions, and the relation between operators and existing formulas. This is an isovalue map of eigenfunctions of a Laplaician on sphere, we transform the domain to aviod singularity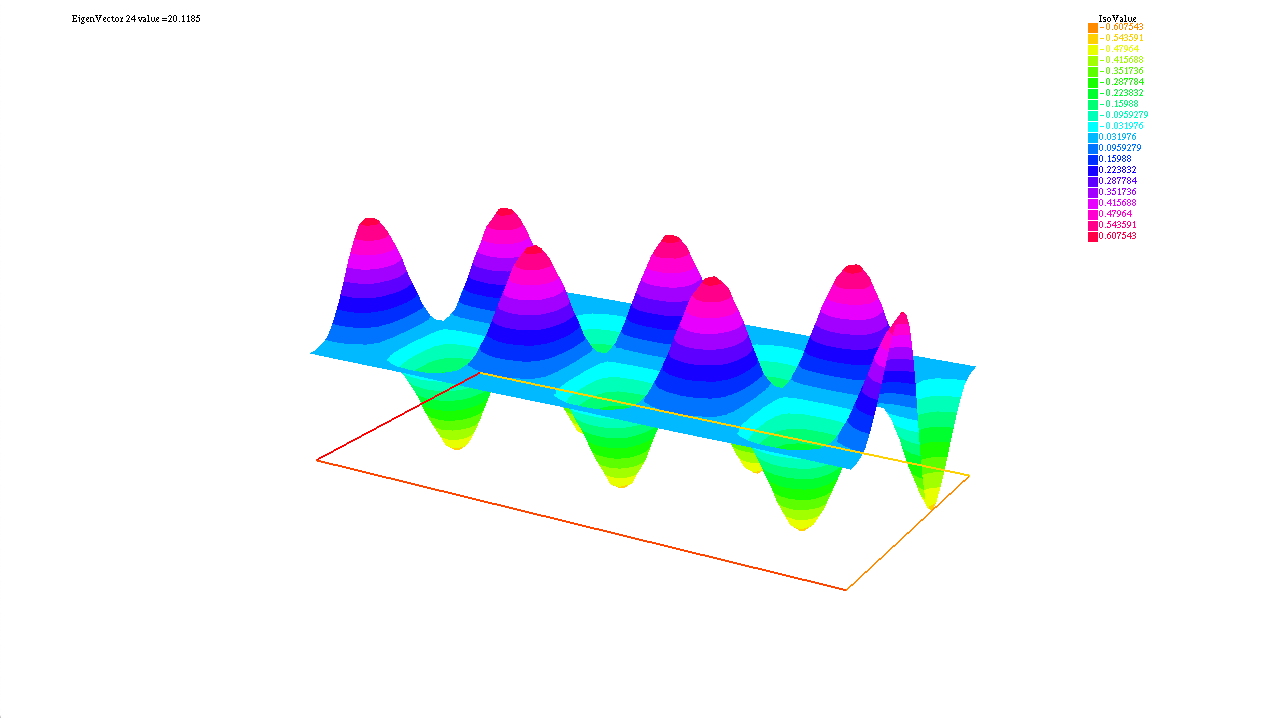
This is another transformation. We transform that to $E^2$ space

An idea is, if we could extend this work to SDE systems comprehensively, many random systems could be described as well. For example, for prediction of financial derivates, greeks are what we utilised. But greeks may not contain as much information as is necessary sometimes for decision making. Spectrum simply have more information, but donot contribute to massive computation. Hence, it could be viewed as a supplement information for trading.